Phần 4 - Giải thích chi tiết kiến trúc mô hình YOLO
Trước tiên để hiểu được kiến trúc này bạn cần có kiến thức về mạng CNN. Xem thêm chi tiết về mạng này tại đây.
Kiến trúc của mô hình YOLO sử dụng các lớp tích chập (Convolution), lớp MaxPooling để đưa từ ảnh đầu vào có chiều (448, 448, 3) và chiều (7, 7, 30). Tại sao kết quả có chiều này thì mình đã miêu tả rất rõ ràng trong bài viết phần 2.

1) Cách tính chiều đầu ra của lớp tích chập
Lớp tích chập là gì được miêu tả chi tiết ở đây.
1.1) Tính toán chiều dài, chiều cao, số kênh của đầu ra


1.2) Diễn giải công thức
Tính chiều đầu ra
Chiều dài
chiều dài đầu ra = [ (chiều dài đầu vào) - (chiều dài của bộ lọc) + 2 x (số padding) ] / (bước nhảy) + 1
Chiều cao
chiều cao đầu ra = [ ( chiều cao đầu vào) - (chiều cao của bộ lọc) + 2 x (số padding) ] / (bước nhảy) + 1
Số kênh đầu ra = Số bộ lọc
2) Cách tính chiều đầu ra của lớp Maxpooling
Xem chi tiết cách lớp Maxpooling hoạt động tại đây.

Tính chiều đầu ra
Thông thường chiều của bộ lọc của maxpool là (2, 2) làm cho chiều dài và rộng của đầu vào đều giảm đi 2.
Trong hình bạn thấy chiều của đầu vào là (4,4) và chiều đầu ra là (2, 2).
3) Kiến trúc của mô hình YOLO
Ví dụ ở lớp tích chập đầu tiên:
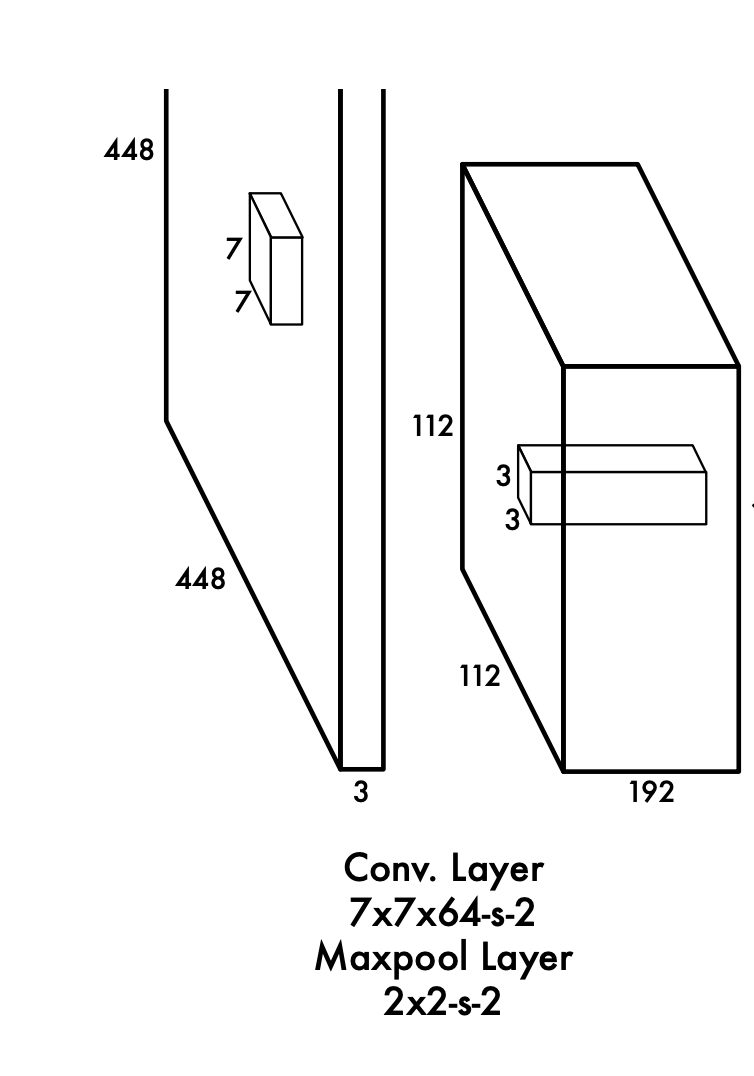
Đầu vào (448, 448, 3)
Thực hiện phép tích chập với 64 bộ lọc cỡ (7,7). Số bước nhảy S=2
Áp dụng công thức để tính chiều của đầu ra
Chiều dài đầu ra = [ (chiều dài đầu vào) - (chiều dài của bộ lọc) + 2 x (số padding) ] / (bước nhảy) = (448 - 7 + 2 x 3) // 2 + 1 = 224
Chiều cao đầu ra = [ ( chiều cao đầu vào) - (chiều cao của bộ lọc) + 2 x (số padding) ] / (bước nhảy) + 1 = (448 - 7 + 2 x 3) // 2 + 1 = 224
Số kênh của đầu ra = Số bộ lọc = 64
Vậy kết luận đầu ra có chiều là (224, 224, 64)
Ở lớp Maxpool tiếp theo:
Đầu vào (224, 224, 64)
Thực hiện phép Maxpool với chiều (2,2) và số bước nhảy là 2
Chiều dài đầu ra: 224 / 2 = 112
Chiều cao đầu ra: 224 / 2 = 112
Vậy kết luận đầu ra có chiều là (112, 112, 64)
Ở lớp tích chập tiếp theo:
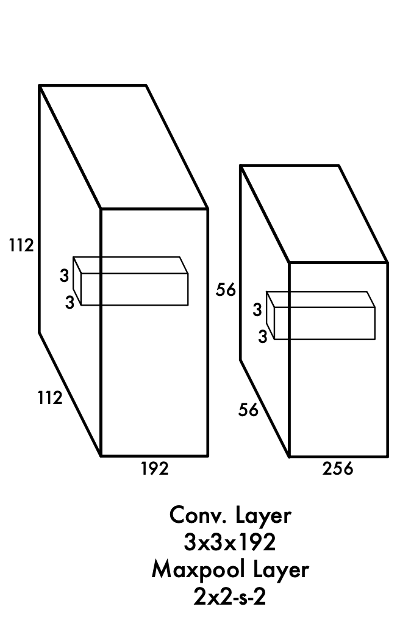
Đầu vào (112, 112, 64)
Thực hiện phép tích chập với 192 bộ lọc cỡ (3, 3). Số bước nhảy S=1
Chiều dài đầu ra = [ (chiều dài đầu vào) - (chiều dài của bộ lọc) + 2 x (số padding) ] / (bước nhảy) = (112 - 3 + 2 x 1) // 1 + 1 = 112
Chiều cao đầu ra = [ ( chiều cao đầu vào) - (chiều cao của bộ lọc) + 2 x (số padding) ] / (bước nhảy) + 1 = (112 - 3 + 2 x 1) // 1 + 1 = 112
Số kênh của đầu ra = Số bộ lọc = 192
Vậy kết luận đầu ra có chiều là (112, 112, 192)
Phân tích lớp tích chập dùng bộ lọc (1, 1):

Thường bộ lọc (1, 1) dùng để giữ chiều dài, chiều cao và thay đổi số kênh của feature map
Đầu vào (56, 56, 256)
Thực hiện phép tích chập với 128 bộ lọc cỡ (1, 1). Số bước nhảy S=1
Chiều dài đầu ra = [ (chiều dài đầu vào) - (chiều dài của bộ lọc) + 2 x (số padding) ] / (bước nhảy) = (56 - 3 + 2 x 1) // 1 + 1 = 56
Chiều cao đầu ra = [ ( chiều cao đầu vào) - (chiều cao của bộ lọc) + 2 x (số padding) ] / (bước nhảy) + 1 = (56 - 3 + 2 x 1) // 1 + 1 = 56
Số kênh của đầu ra = Số bộ lọc = 128
Vậy kết luận đầu ra có chiều là (56, 56, 128)
Lớp cuối cùng:

Đầu vào (4096,)
Thực hiện một lớp nhân ma trận + hàm phí tuyển để tạo ra chiều (1470,). Chiều này tương đồng với chiều (7, 7, 30) đã được nhắc tới trong phần 2.
3) Cách thức lập trình mô hình
Trong bài này chúng ta sẽ sử dụng Pytorch để lập trình mô hình
Chi tiết mô hình được lập trình theo hình vẽ bên trên
import torch
import torch.nn as nn
from torchvision.models import resnet50, ResNet50_Weights
class YOLOv1(nn.Module):
def __init__(self):
super().__init__()
self.depth = B * 5 + C
layers = [
nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3), # Conv 1
nn.LeakyReLU(negative_slope=0.1),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(64, 192, kernel_size=3, padding=1), # Conv 2
nn.LeakyReLU(negative_slope=0.1),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(192, 128, kernel_size=1), # Conv 3
nn.LeakyReLU(negative_slope=0.1),
nn.Conv2d(128, 256, kernel_size=3, padding=1),
nn.LeakyReLU(negative_slope=0.1),
nn.Conv2d(256, 256, kernel_size=1),
nn.LeakyReLU(negative_slope=0.1),
nn.Conv2d(256, 512, kernel_size=3, padding=1),
nn.LeakyReLU(negative_slope=0.1),
nn.MaxPool2d(kernel_size=2, stride=2)
]
for i in range(4): # Conv 4
layers += [
nn.Conv2d(512, 256, kernel_size=1),
nn.Conv2d(256, 512, kernel_size=3, padding=1),
nn.LeakyReLU(negative_slope=0.1)
]
layers += [
nn.Conv2d(512, 512, kernel_size=1),
nn.Conv2d(512, 1024, kernel_size=3, padding=1),
nn.LeakyReLU(negative_slope=0.1),
nn.MaxPool2d(kernel_size=2, stride=2)
]
for i in range(2): # Conv 5
layers += [
nn.Conv2d(1024, 512, kernel_size=1),
nn.Conv2d(512, 1024, kernel_size=3, padding=1),
nn.LeakyReLU(negative_slope=0.1)
]
layers += [
nn.Conv2d(1024, 1024, kernel_size=3, padding=1),
nn.LeakyReLU(negative_slope=0.1),
nn.Conv2d(1024, 1024, kernel_size=3, stride=2, padding=1),
nn.LeakyReLU(negative_slope=0.1),
]
for _ in range(2): # Conv 6
layers += [
nn.Conv2d(1024, 1024, kernel_size=3, padding=1),
nn.LeakyReLU(negative_slope=0.1)
]
layers += [
nn.Flatten(),
nn.Linear(S * S * 1024, 4096), # Linear 1
nn.Dropout(),
nn.LeakyReLU(negative_slope=0.1),
nn.Linear(4096, S * S * self.depth), # Linear 2
]
self.model = nn.Sequential(*layers)
def forward(self, x):
return torch.reshape(
self.model.forward(x),
(x.size(dim=0), S, S, self.depth)
)Để in ra kiến trúc của mô hình kèm đầu ra và đầu vào, bạn có thể sử dụng thư viện torch-summary để hiển thị.
Với đoạn code hiển thị như sau:
from torchsummary import summary
model = YOLOv1()
summary(model, (3, 448, 448))Kết quả in ra:
 Bạn có thể học lập trình và kiểm tra kích cỡ các lớp song song với nhau để đảm bảo bạn đang thực hiện chính xác.
Bạn có thể học lập trình và kiểm tra kích cỡ các lớp song song với nhau để đảm bảo bạn đang thực hiện chính xác.
Vậy là team đã trình bày xong được kiến trúc của mô hình YOLO. Trong bài tiếp theo chúng tôi sẽ giải thích chi tiết hàm mất mát của mô hình này.
Bạn cùng theo dõi nhé.
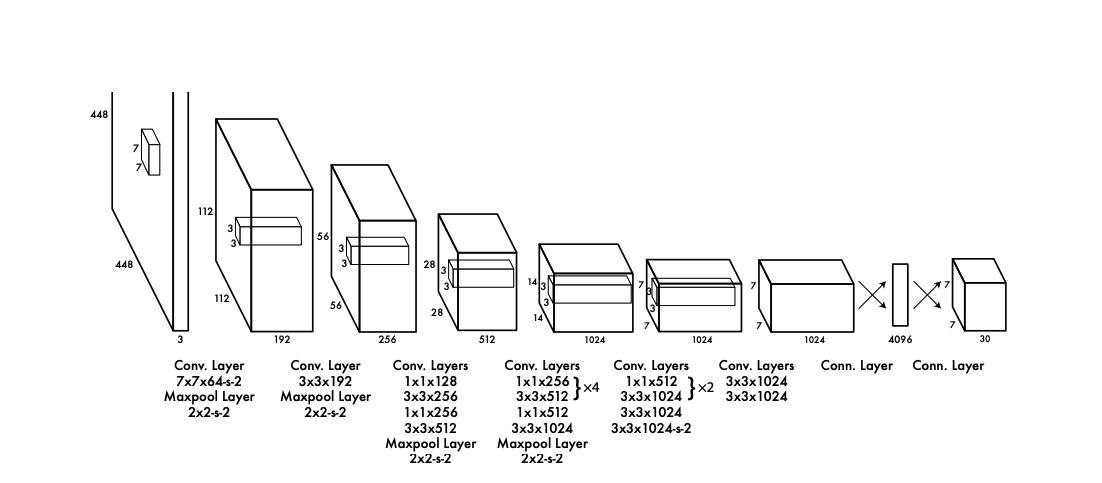 Nguồn ảnh
Nguồn ảnh